Before starting this assignment, I thought about what I was going to do.
First, regarding the choice of the scoring function, I believe that complex scoring will only provide minor improvements in quantity and cannot decisively improve quality, so I chose the simplest L2 norm.
Second, before reading the details on the course website, I realized that the intensity between different channels does not have much comparative value. Once the image is quite colorful, the intensity-based L2 norm will fail. Obviously, edge extraction is necessary, and I don’t even plan to try methods that do not extract edges. As for the pyramid method, it is a must.
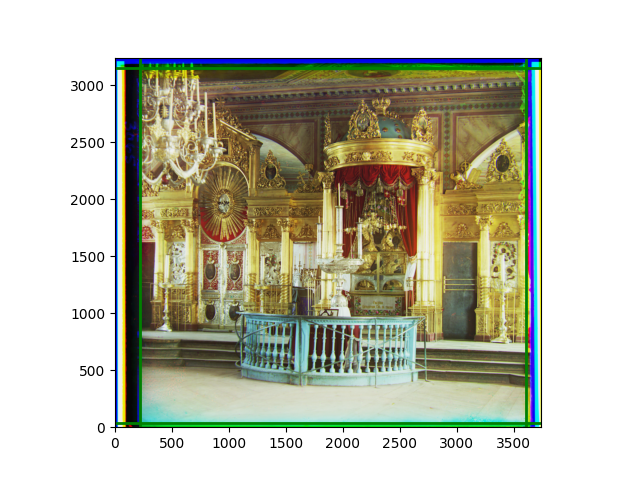
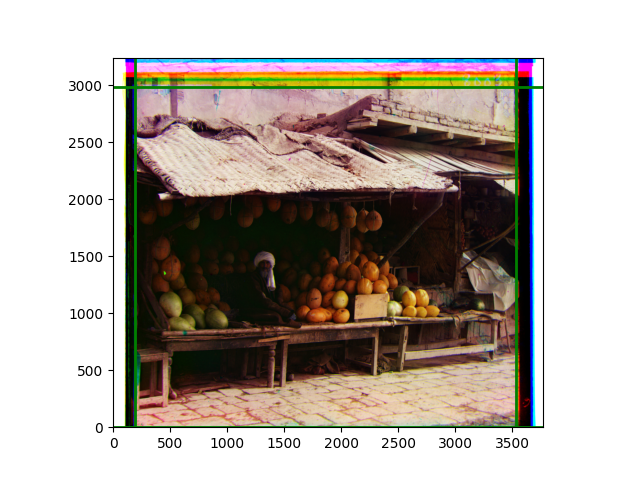
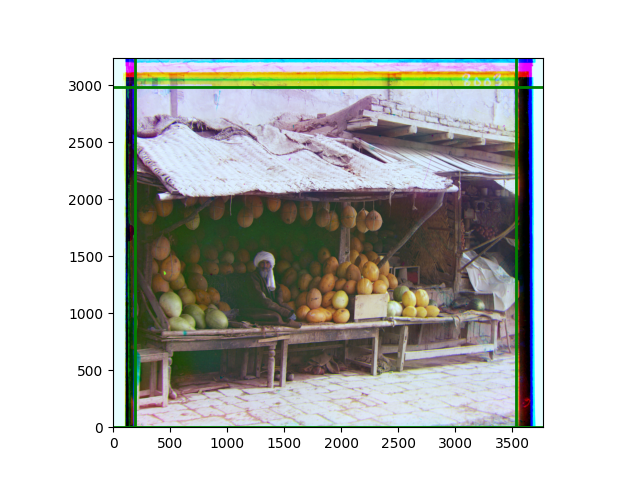
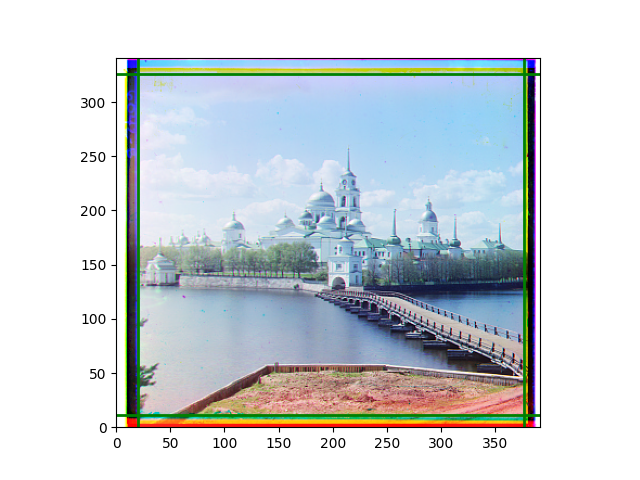
Third, for edge cropping, I believe it should be done by channel, combined with the offsets obtained from each channel for mathematical operations. To clearly show the accuracy of the cropping, I plan to draw the lines to be cropped on each channel or the overlaid image, rather than actually cropping the edges. There are also some new phenomena discovered during the experiments, which will be explained in the subsequent explanation of the experimental process.
Finally, I thought of a promising method to handle rotation and scaling without incurring significant time costs. Specifically, my idea is to find some small windows with obvious details, perform rough edge alignment at the smallest scaling ratio, and then calculate their offsets in the moved original image. Since these local windows are small, the impact of rotation on them is much smaller than on the entire window. Just like two nails can fix a line, these local windows are the nails between images, and we can find the most likely affine transformation that includes rotation and scaling, or even more complex transformations. Because the small window size is very small, the computational cost is also small. Since rough alignment has already been done, the offsets that these small windows need to try are not large. In suitable cases, the speed may even be faster than the pyramid method. However, this idea encountered some problems in the experiment, which will be explained later.
I also thought of some other possible operations, planning to try them if I could complete the above more mature ideas. However, due to limited time, I had to give up these ideas. I list them as follows.
For noise, considering that the photos of the three channels are relatively independent, and the main noise is black spots, it is reasonable to believe that small black spots or scratches that appear only in one channel are likely to be noise and should be directly replaced with the surrounding average. For “small,” we can use Sobel or Canny to extract edges, then perform Gaussian blur as a mask. For “black,” we also create a mask based on the information of each channel. When both masks meet the conditions, we replace the problematic channel. However, I don’t have a good idea of how to perform smooth interpolation in a two-dimensional irregular area.
For color mapping, I believe it should be done based on the RGB channels separately. For example, the film may have some fading, which corresponds to the strengthening of specific channel signals. Such physical changes may be the main factor for some color tones in the overlaid color image. However, how to multiply each channel by an appropriate factor and then overlay them is not as simple as directly doing ordinary adjustments, so I did white balance and gamma correction.
In the actual experiment, the first problem encountered was the order of the horizontal and vertical dimensions of the image converted to a NumPy array. I initially got it wrong and didn’t figure out the height and width. Although this problem is relatively basic, it took me several hours to debug.
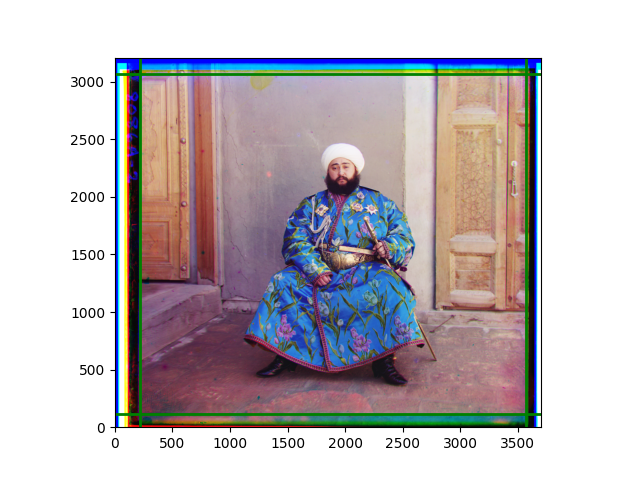
The second problem was that I forgot to include the original size image in the pyramid list at the beginning, so it was not aligned at the original scale. This problem was not easy to find because the “large” image became sufficiently small after only three or four scalings. I originally thought that missing one alignment would not matter, but it did show some artifacts.
The third problem was that some images were not aligned, which was due to the insufficiently large search space at the beginning. Typical examples are the images “melon” and “self-portrait.” There are two solutions: one is to expand the search space in the first step, and the other is to allow some redundancy between steps. I solved the problem with the former. For the latter, as long as the search range decays inversely with the square, the time cost will not be significant. Of course, pre-cropping the overall edges would also be effective, but I don’t want to modify the course framework code.
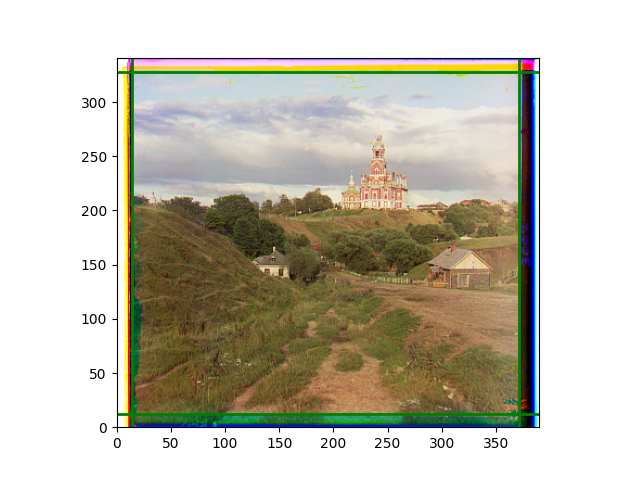
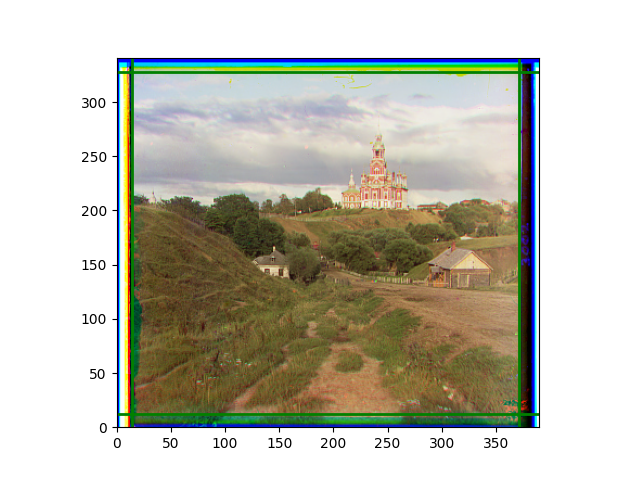
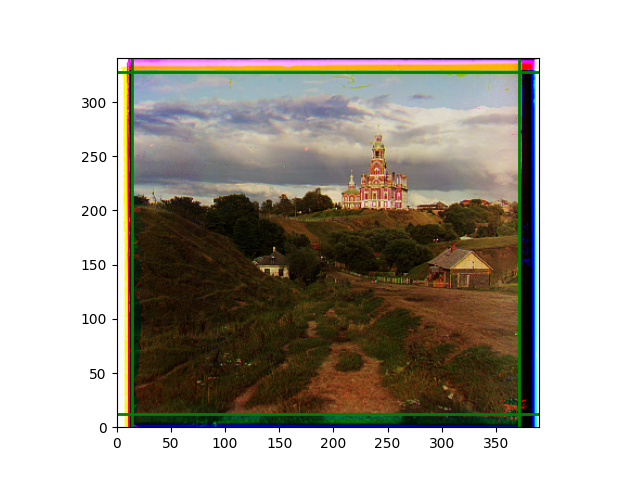
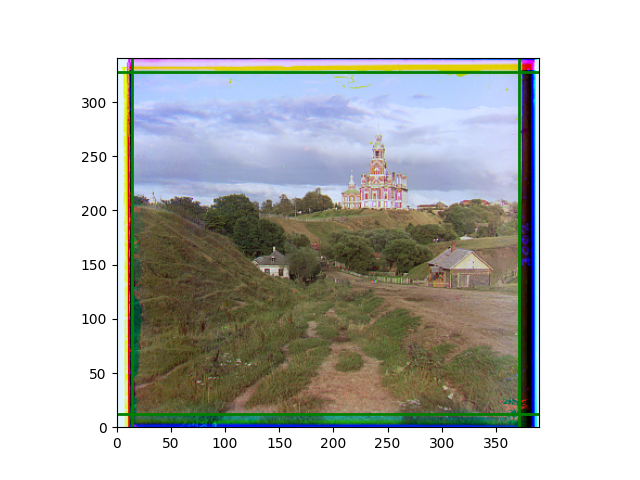
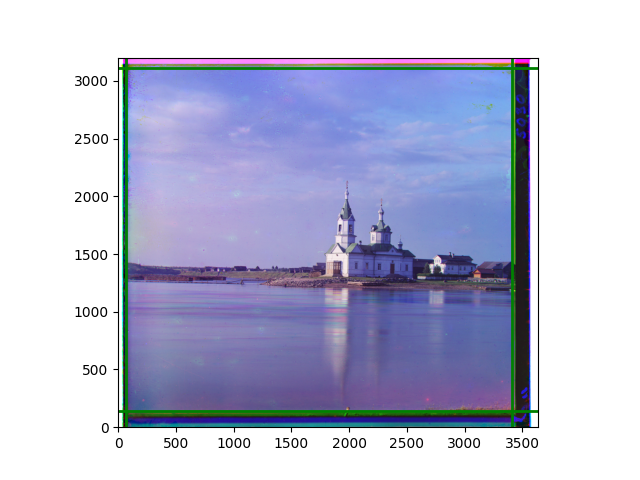
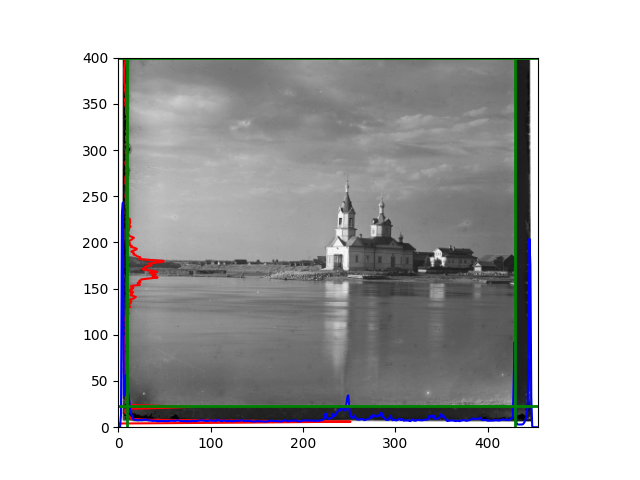
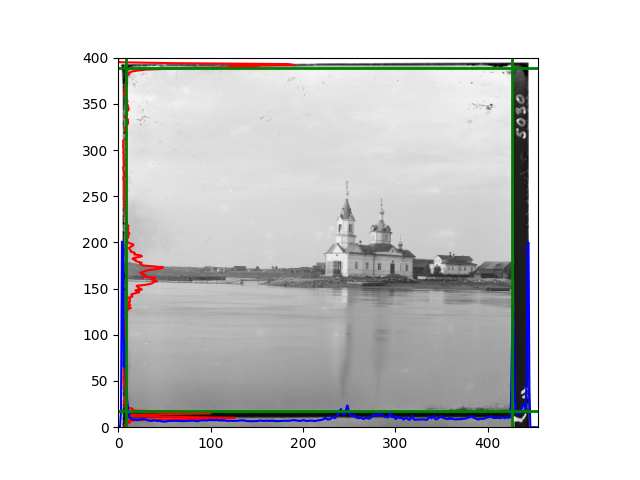
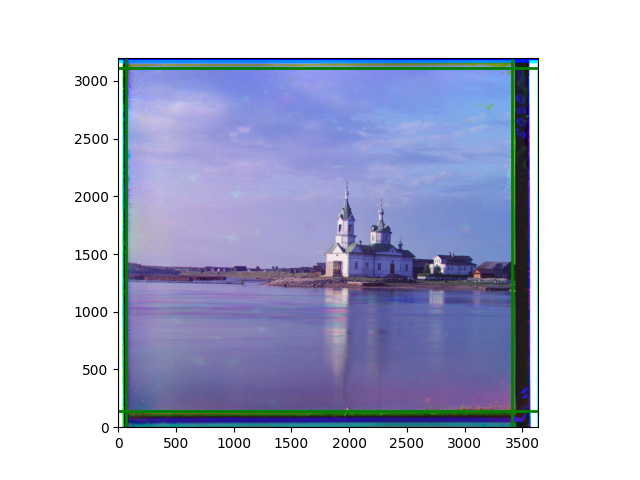
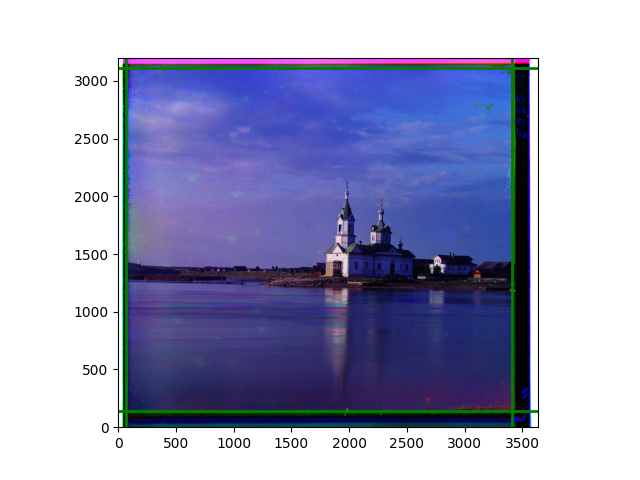
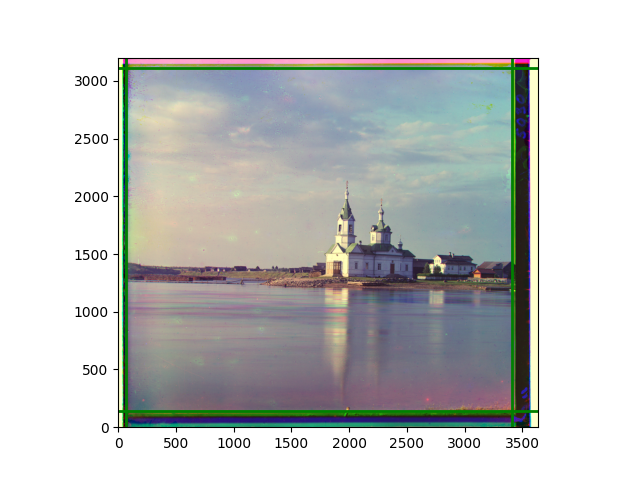
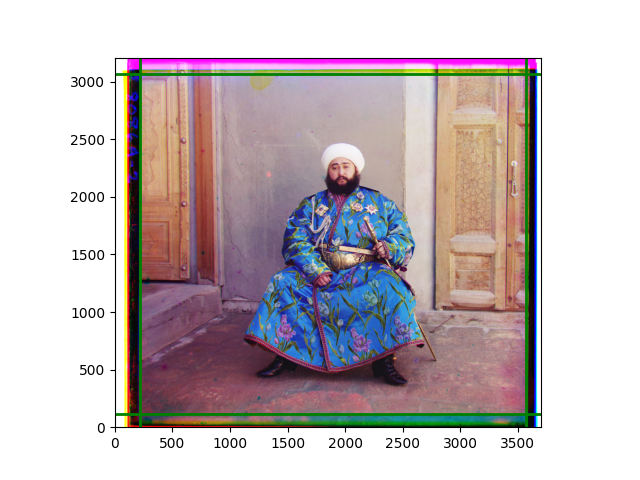
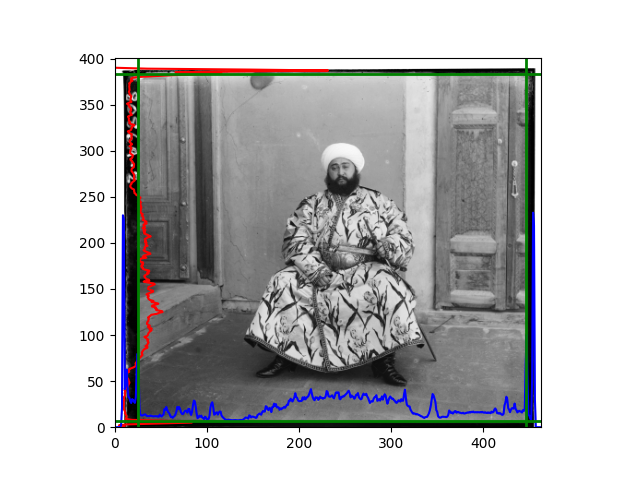
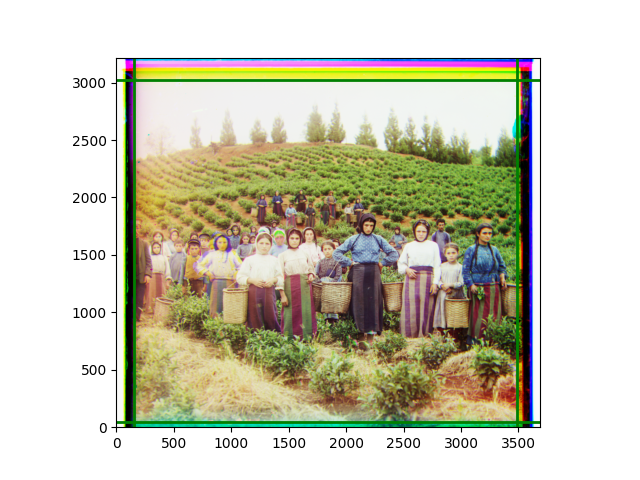
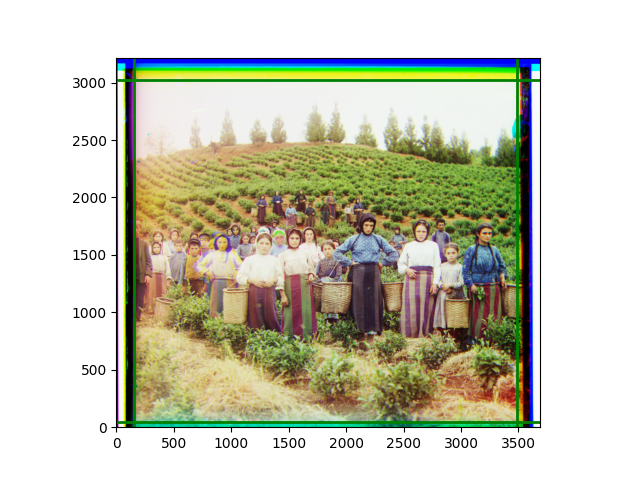
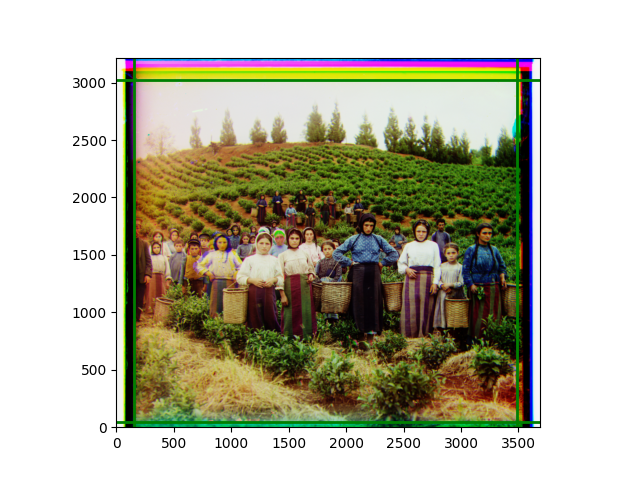
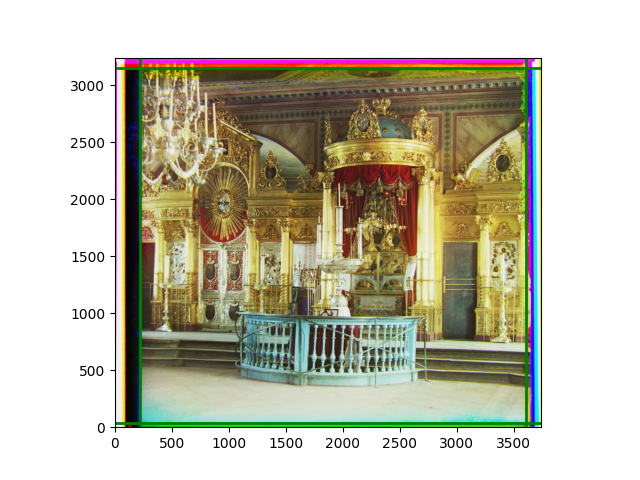
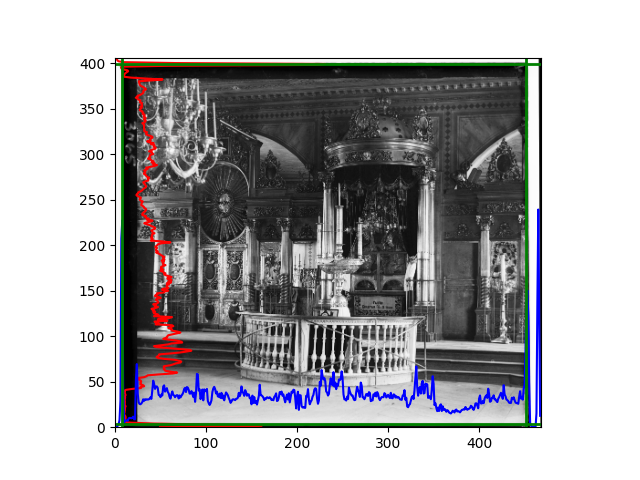
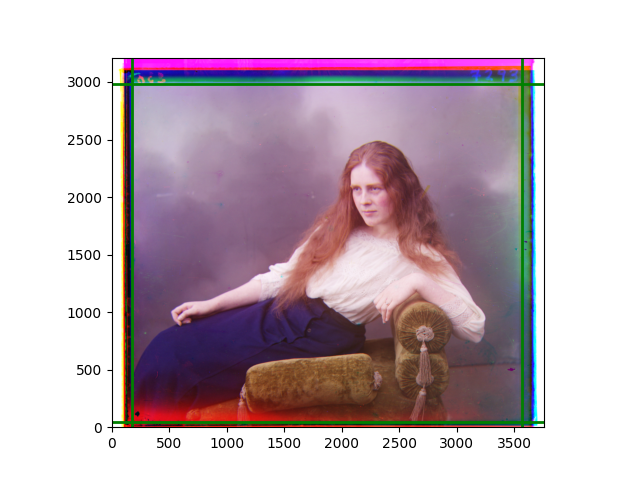
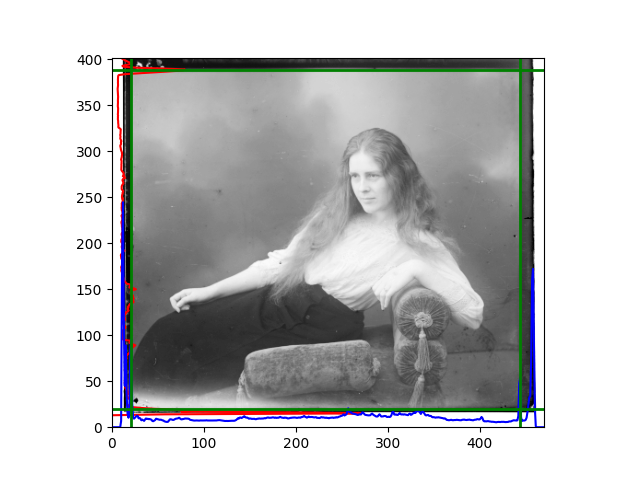
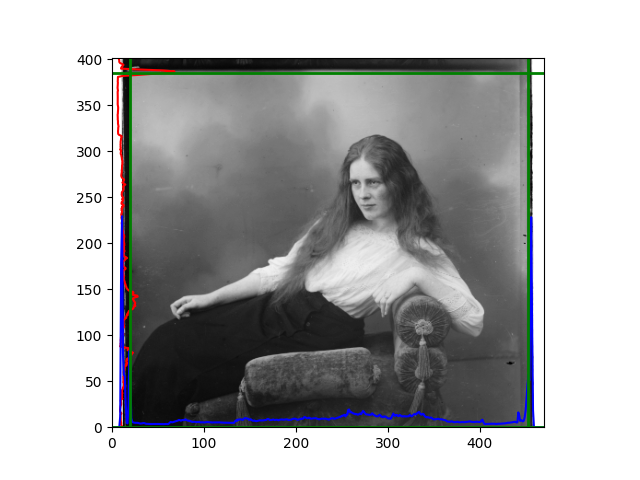
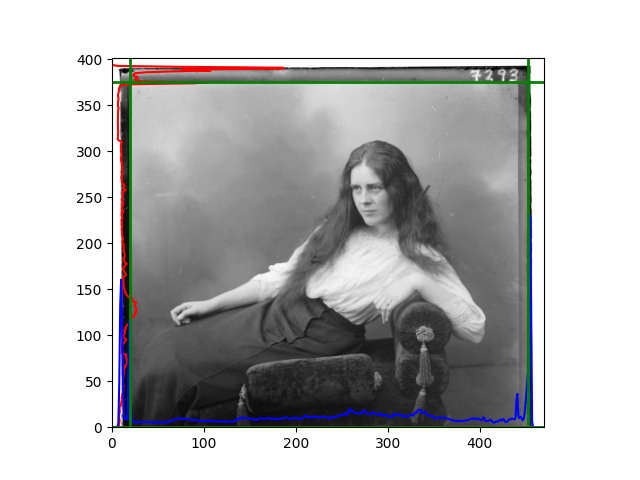
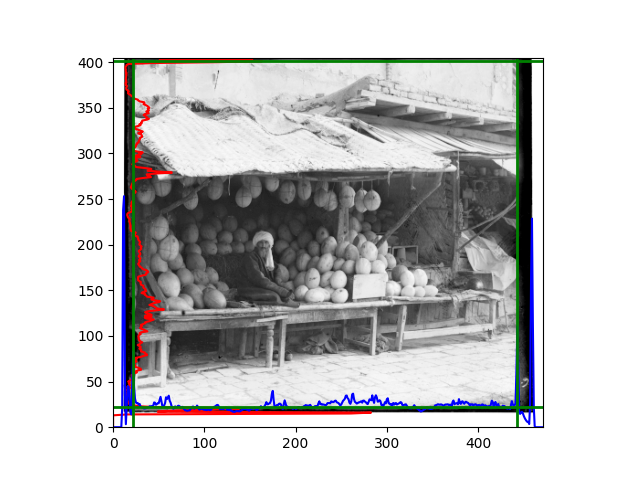
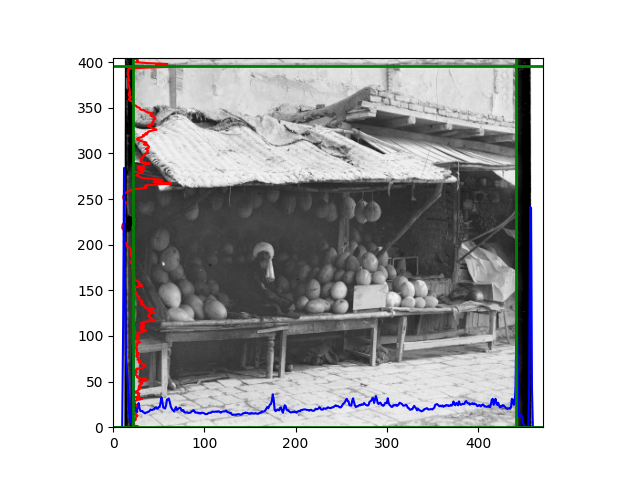
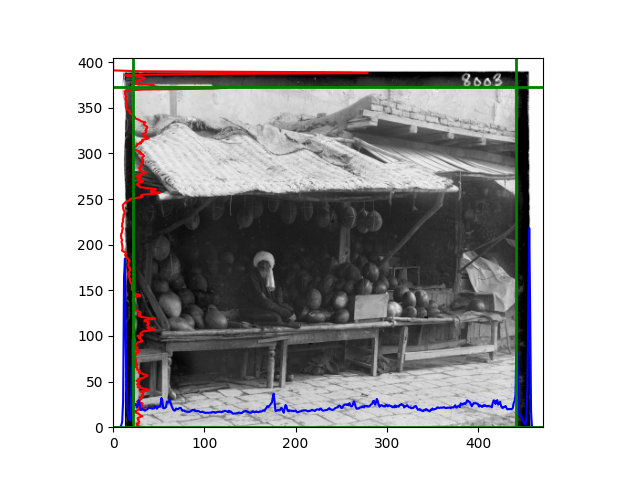
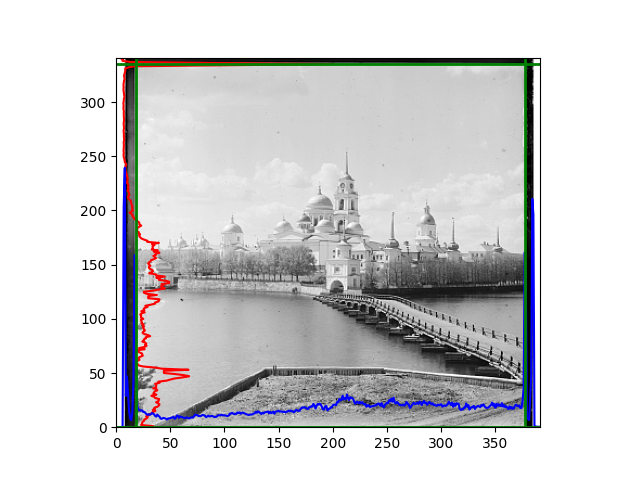
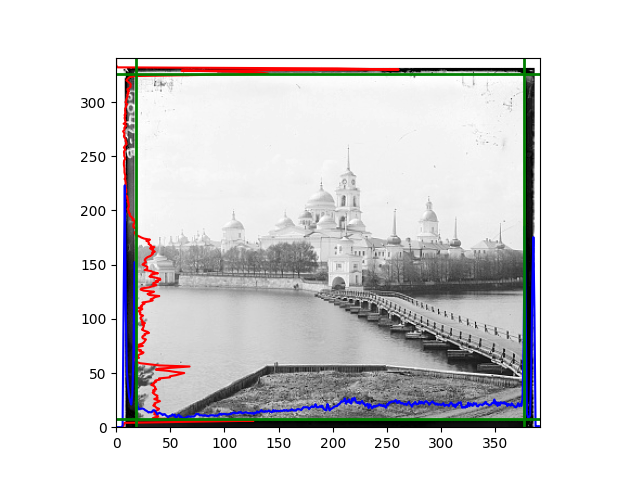
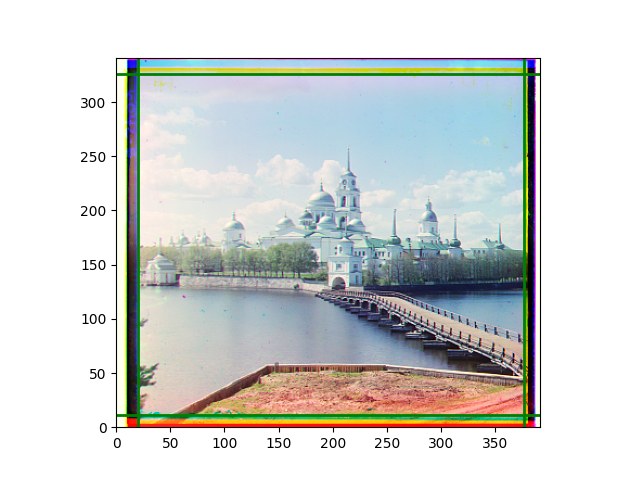
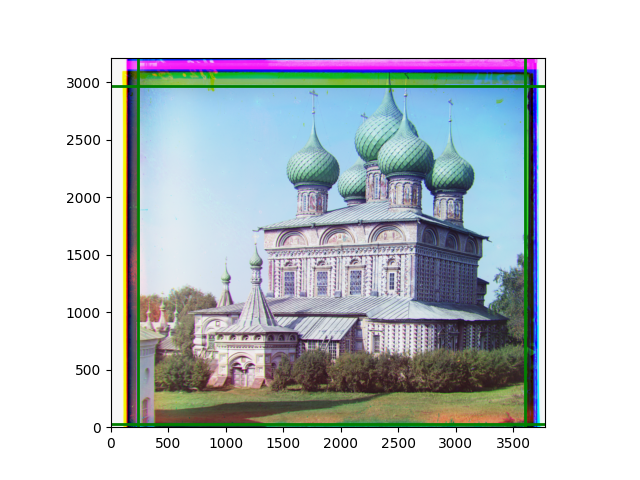
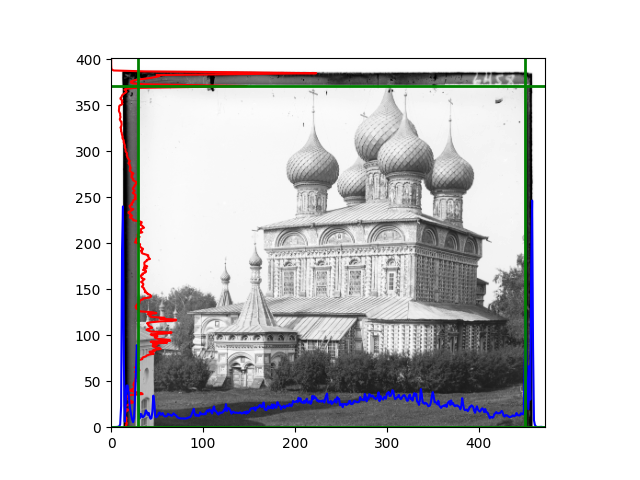
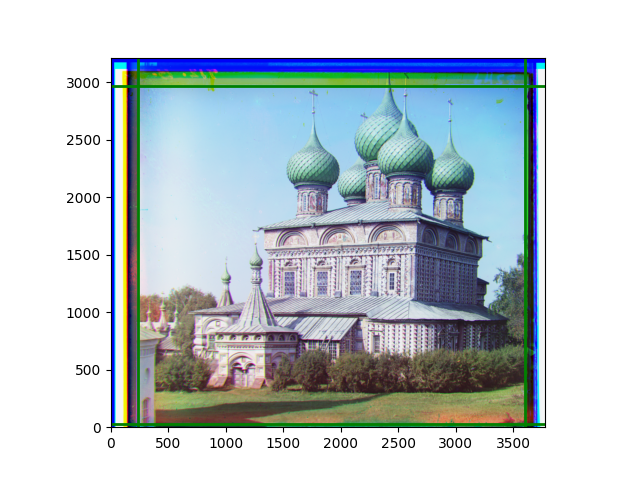
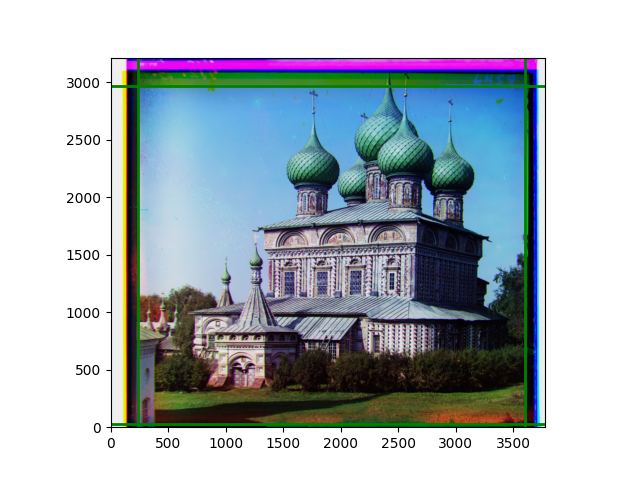
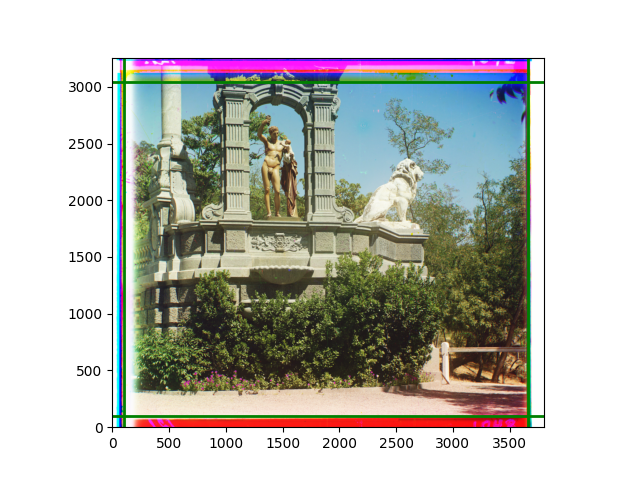
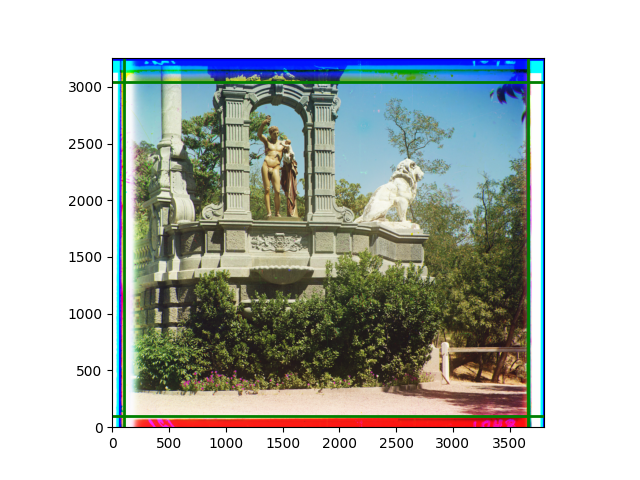
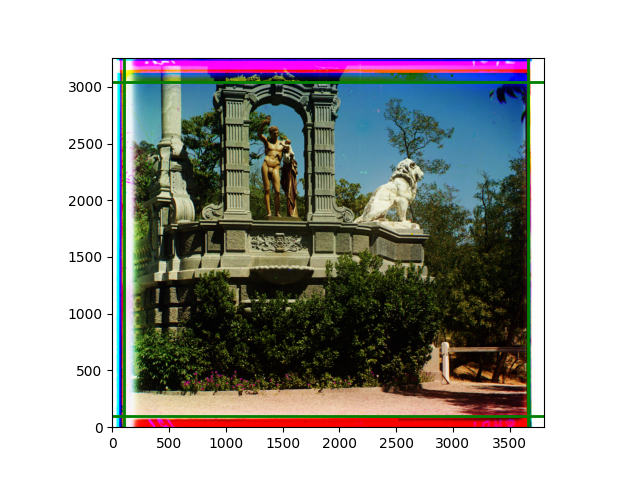
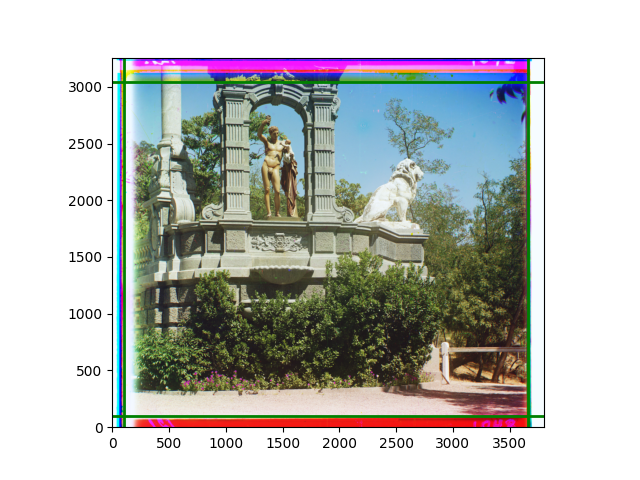
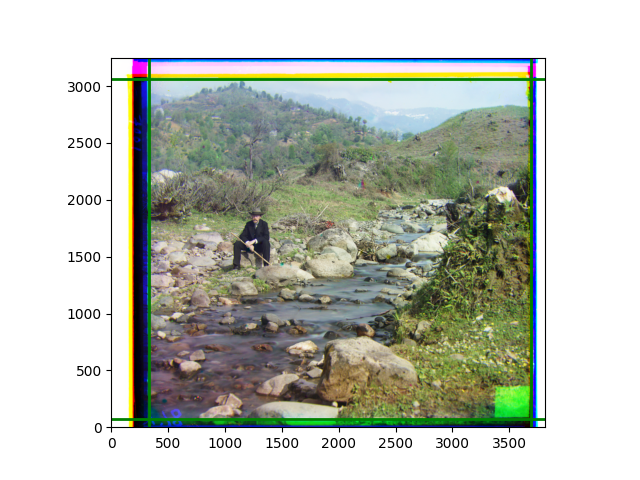
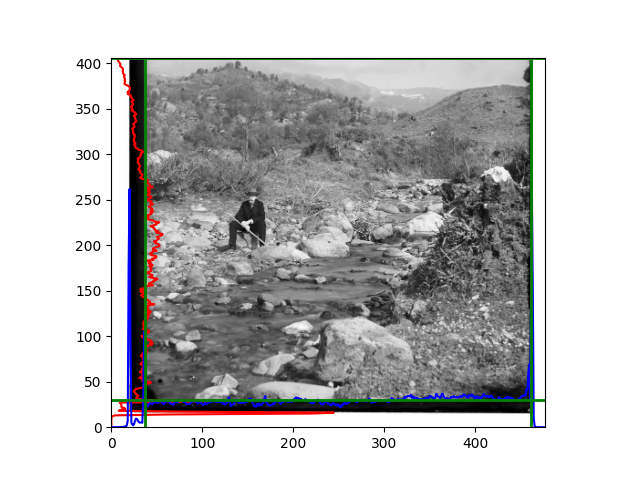
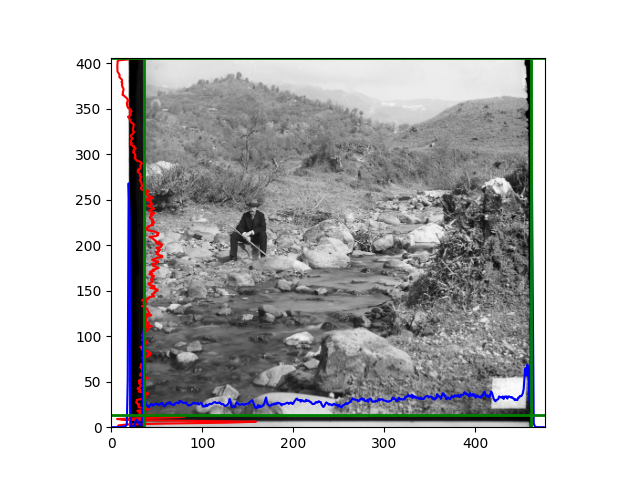
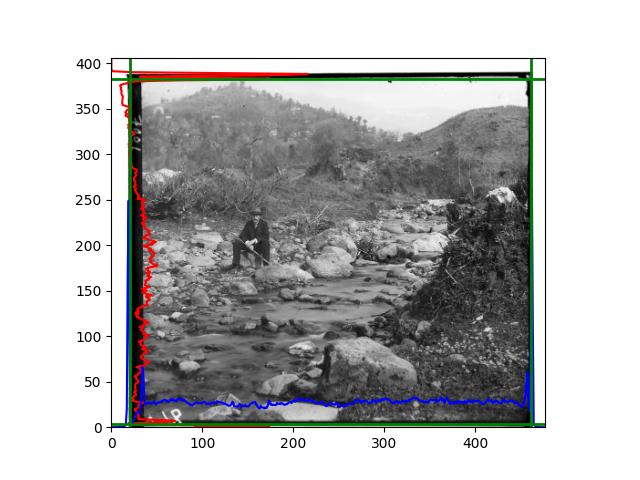
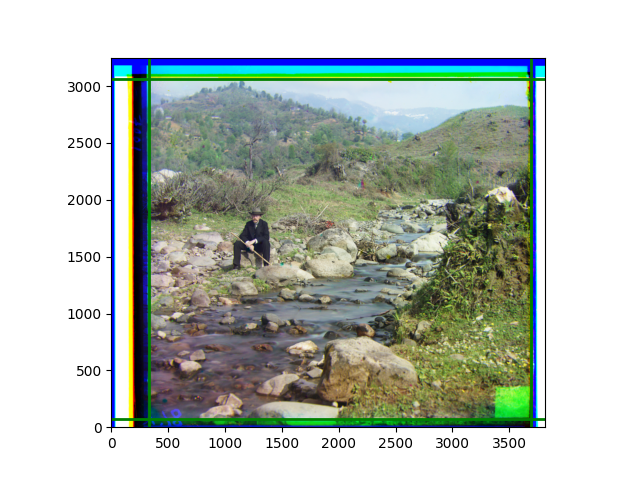
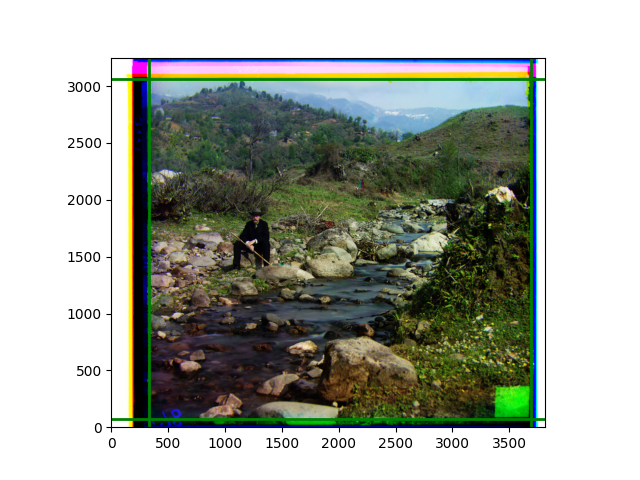
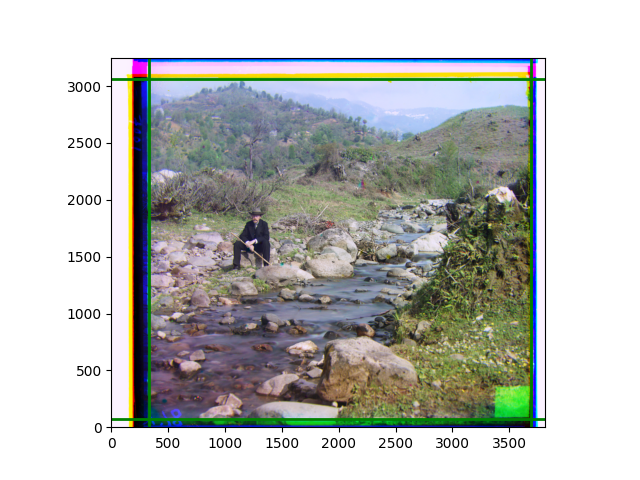
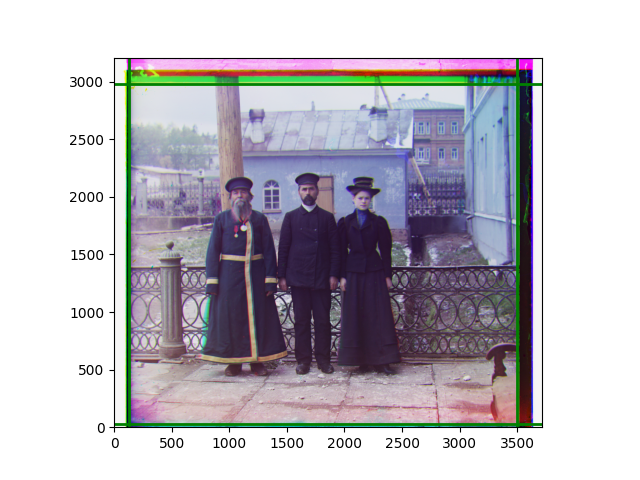
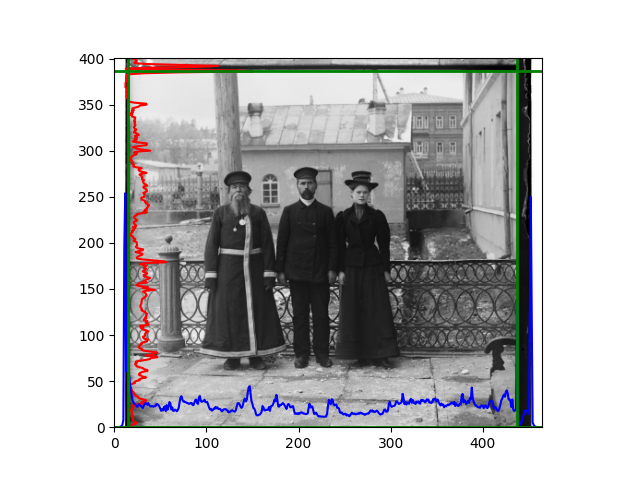
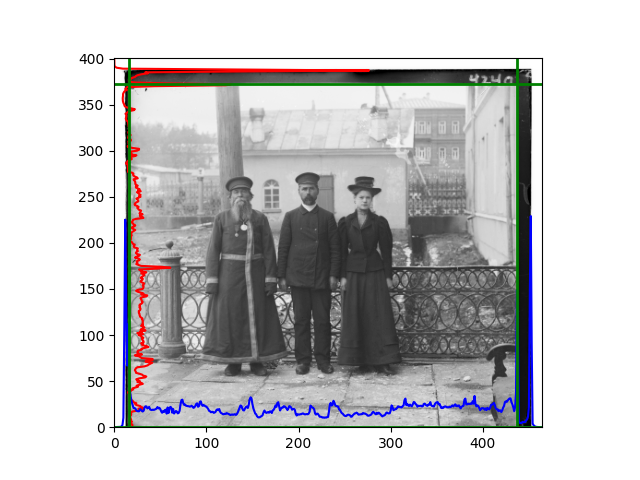
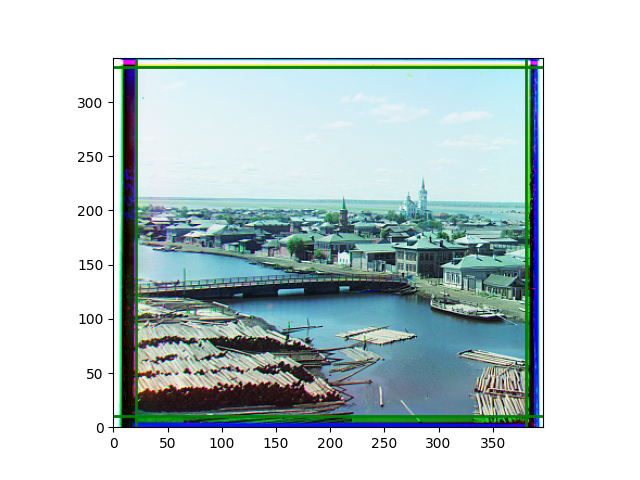
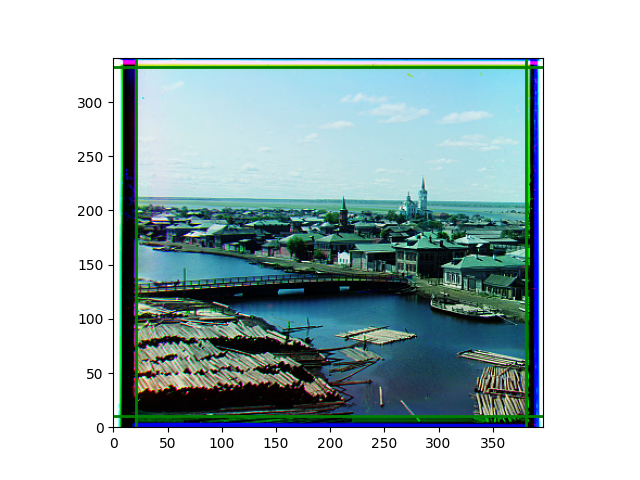
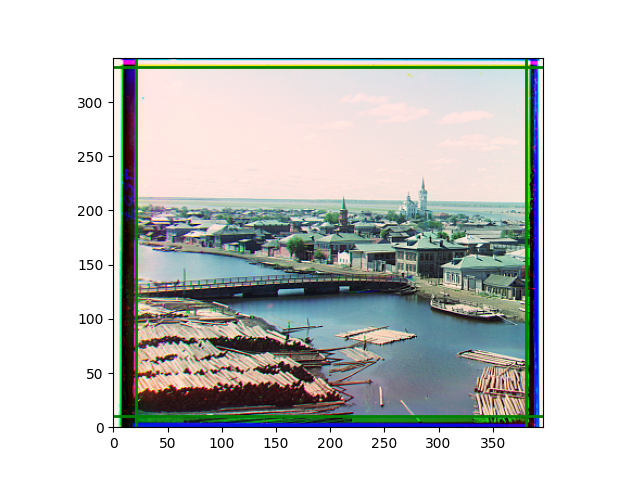
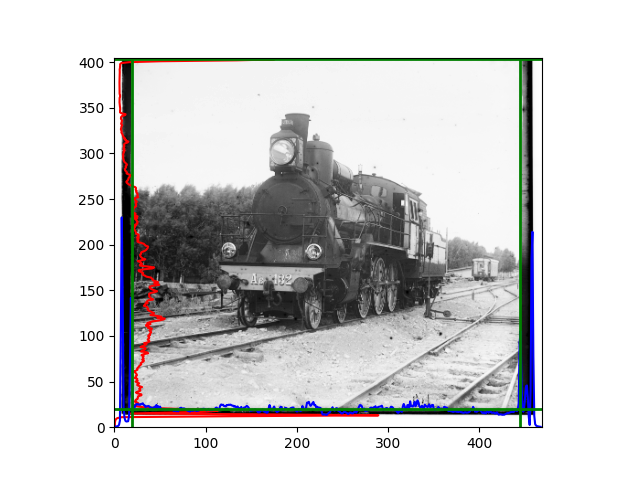
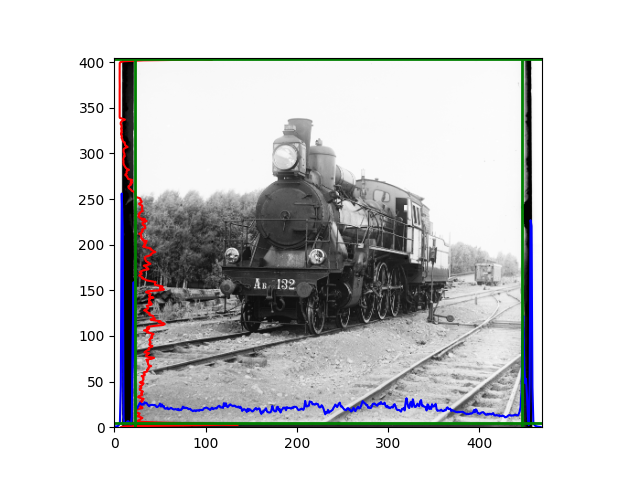
The fourth problem is image cropping. The main borders of the image include black and white edges, and parts with missing information due to offsets also need to be removed. The latter can be easily completed through mathematical calculations, but the former at least requires some effective features to determine. I believe that for the black and white edges of the image, it should be determined within each channel, rather than re-graying the overlaid color image and then processing it. This ensures the prominence of edge information.
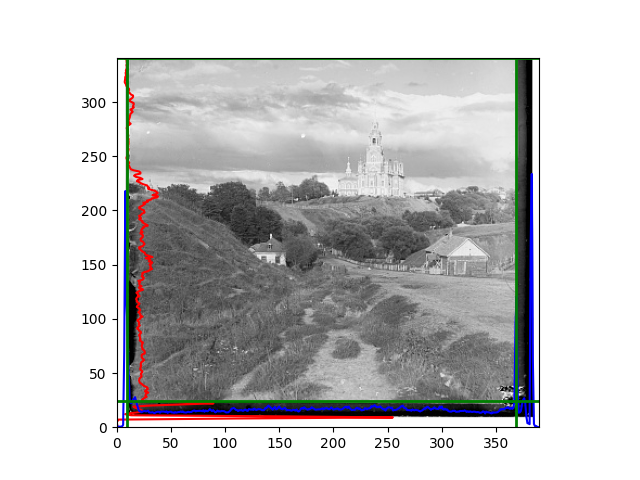
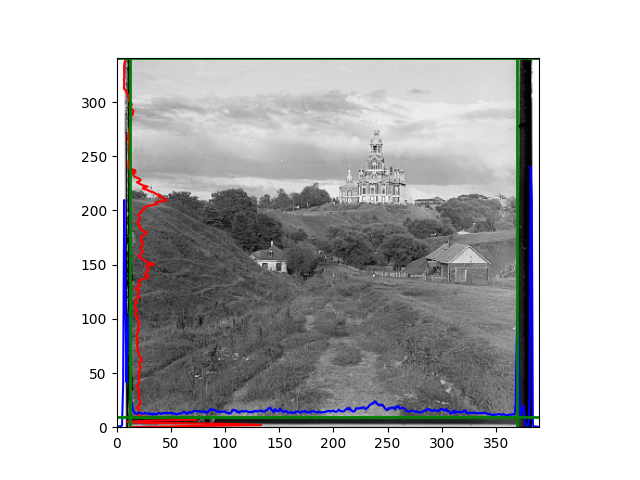
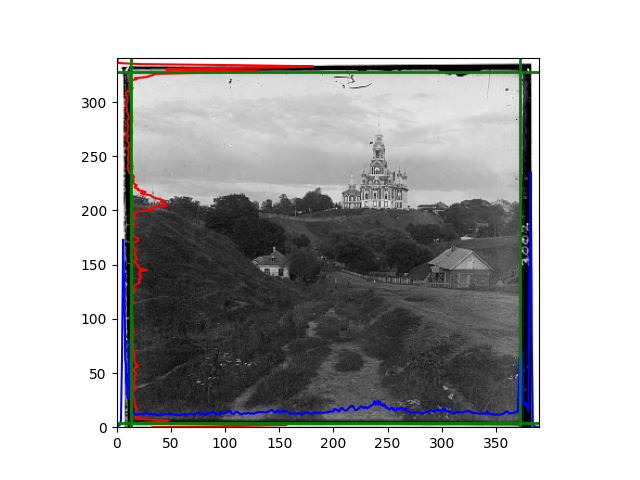
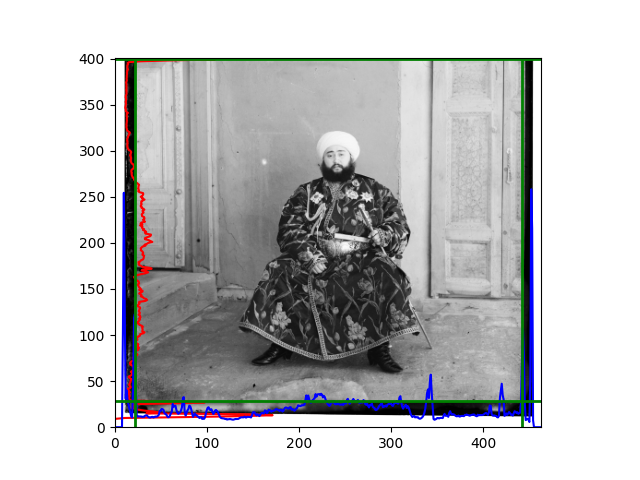
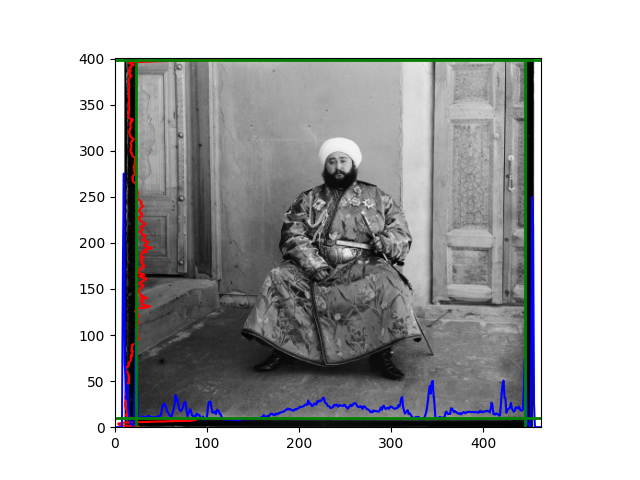
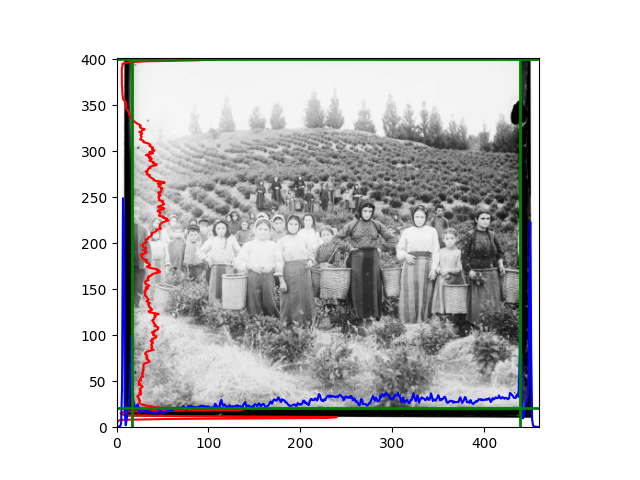
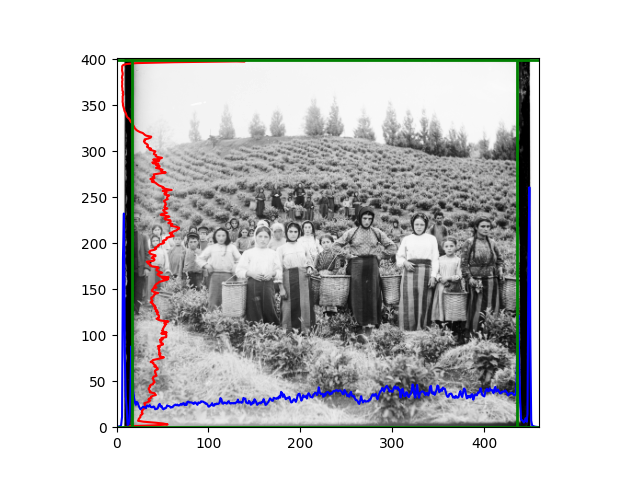
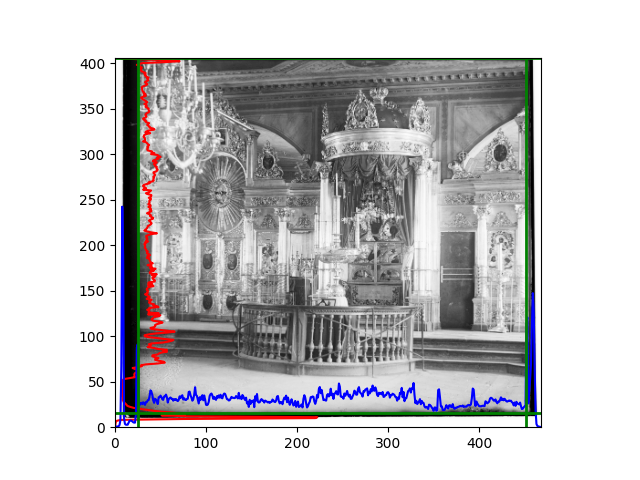
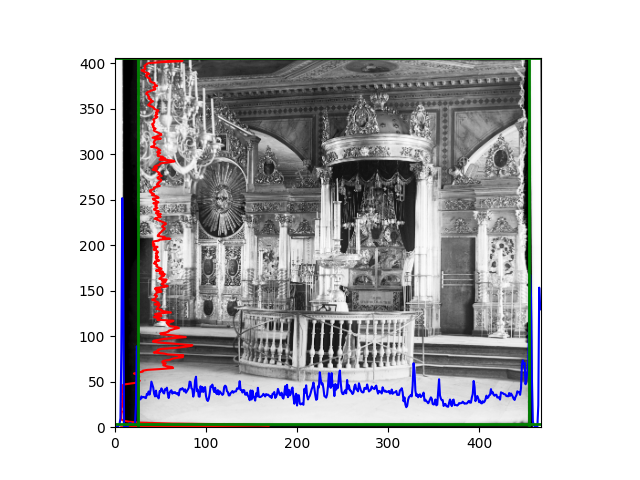
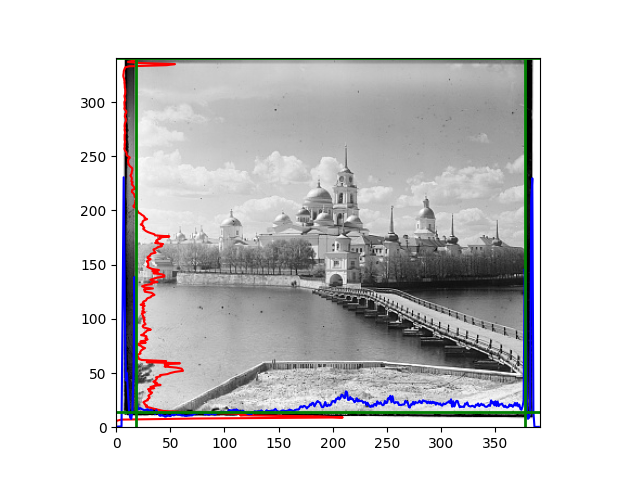
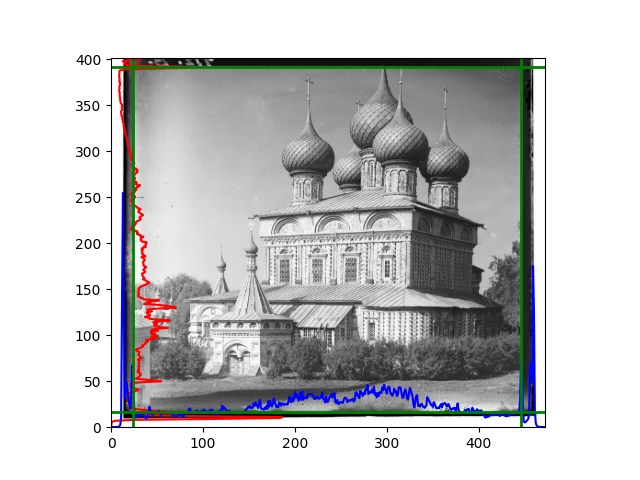
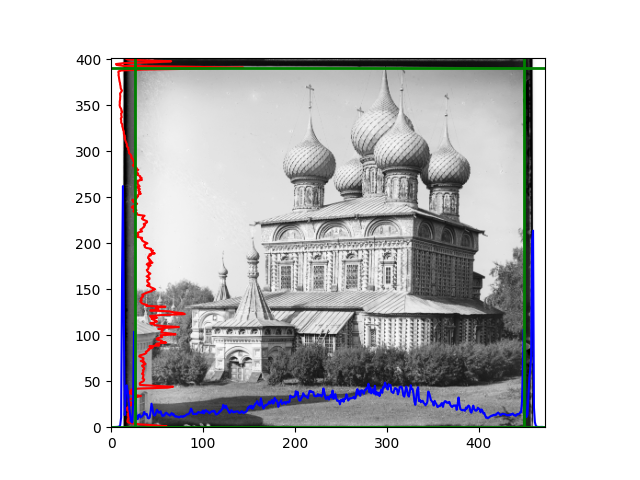
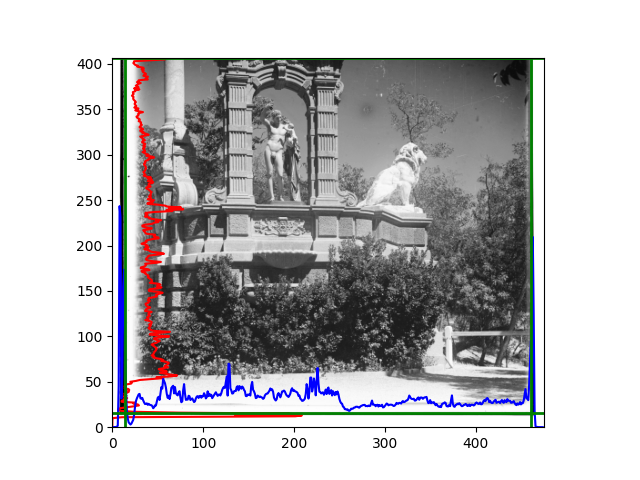
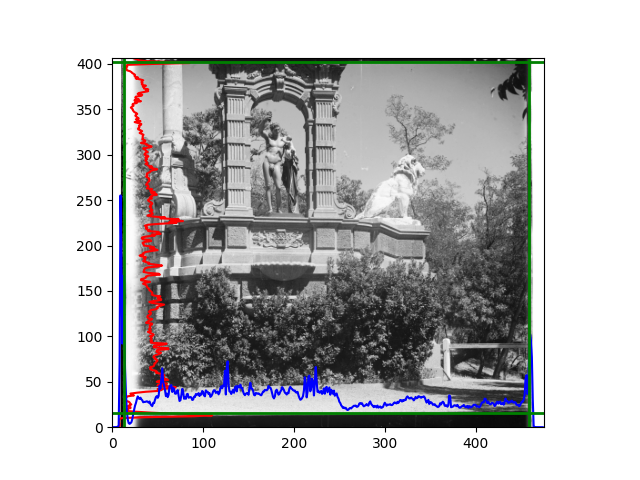
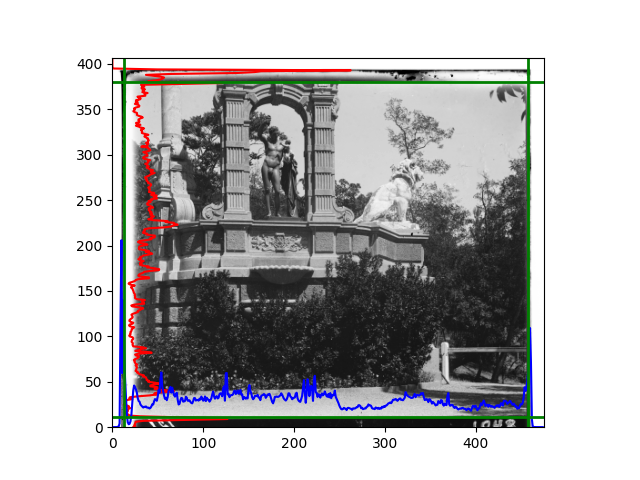
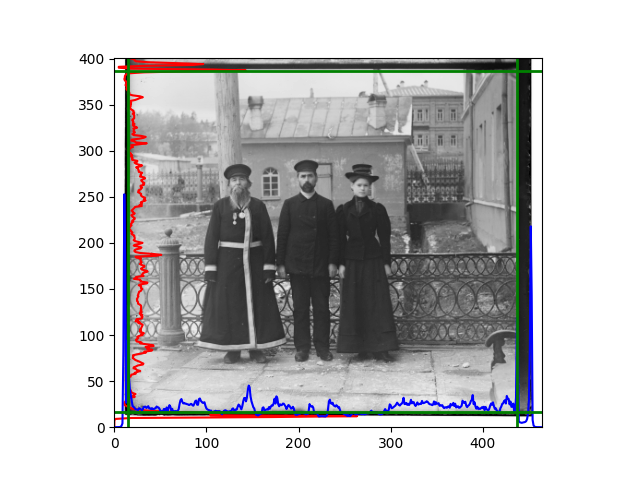
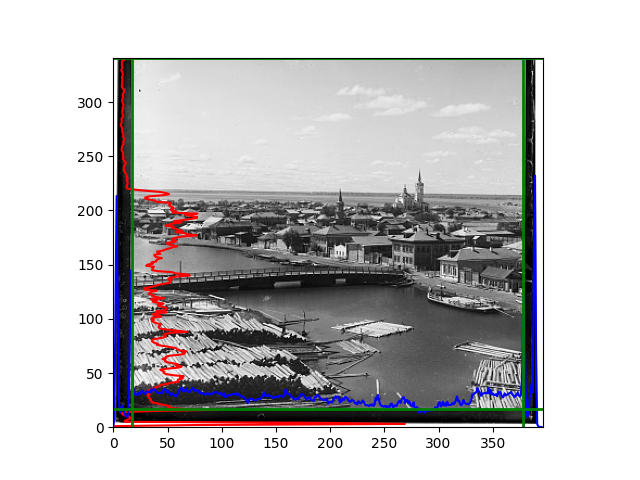
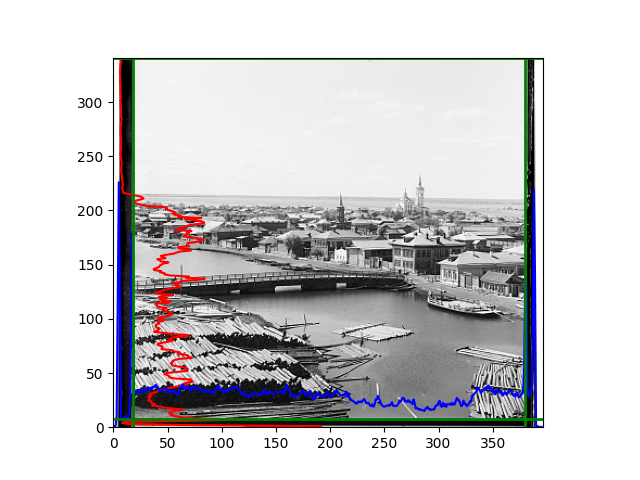
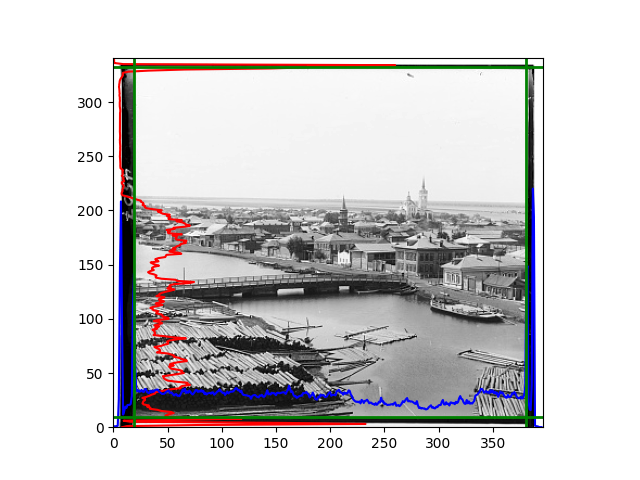
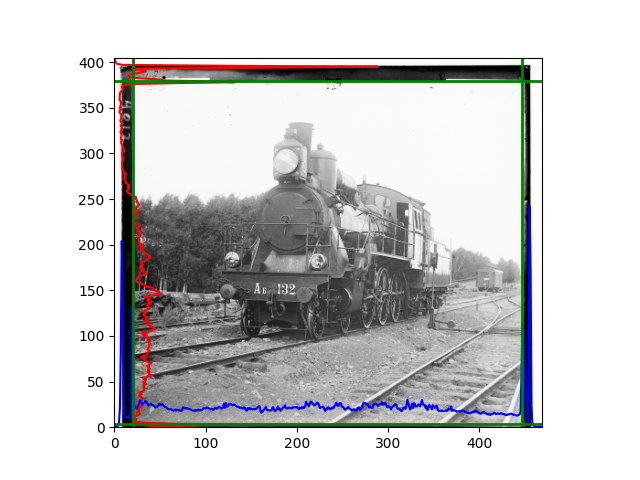
For this problem, I tried various methods. Since manually selecting a threshold requires complex debugging, the code simply chooses the coordinates within a certain range that are closest to the inside and have a statistic higher than the mean plus twice the standard deviation. I tried many statistics, such as the number of very black or very white pixels per column, the gradient of the number of very black or very white pixels per column, the sum of gradients extracted using Sobel per column, the variance of pixel brightness per column, the mean of the variance of pixel brightness segments per column, and various mathematical combinations of the above. To find the most significant feature, I visualized the statistics, and the webpage shows the visualization of the statistics I finally chose and the edges obtained in the current channel. In fact, the simplest is the best. The Sobel gradient and on all channels of the given image, only two edges were misaligned. These two misaligned edges were also at the junction of black and white edges, while the better edges were relatively blurred. Besides, considering that the final cropping will take into account the offsets and edges of the three channels, these extremely rare errors did not affect any final results. Although methods like erosion and dilation would be more intuitive, they would be much slower.
The fifth problem was caused when visualizing the charts mentioned in the fourth problem. The drawn statistics were too small and overlapped with the axis, initially making me think there was an error in the drawing. Although this problem took a long time to debug, it was not of much value. However, it also shows that using the standard deviation for automatic thresholding is very convenient.
The sixth problem was discovered after visualization. The statistical rules calculated for large images were very different from those for small images. The effect of using the sum of Sobel gradients for small images was much better. I believe this is because the changes between adjacent columns in large images are smaller. So I directly reduced the size of the large image.
The seventh problem occurred when I considered combining edges and pyramids. In fact, we can adjust edge cropping like adjusting offsets, but that is too complicated. Although repeatedly scaling the same image indeed wasted time, adding functionality to my fragile pyramid code seemed to cause unnecessary trouble. So I directly avoided this, and the effect still looked good.
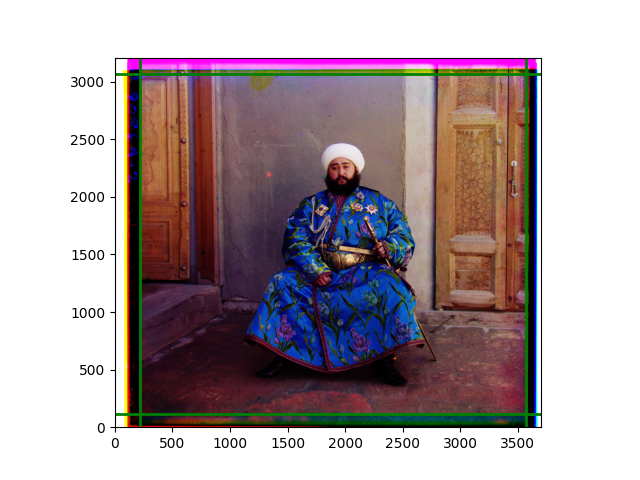
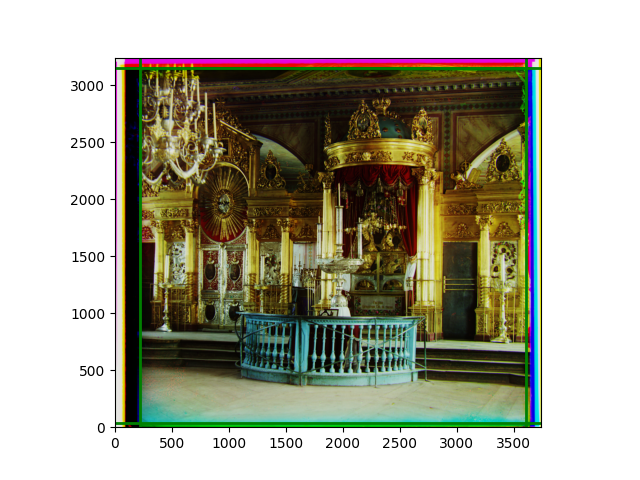
The eighth problem was related to the new method of rotation and scaling I mentioned earlier. I first cropped the edges, then calculated the rough offset of the image, and then divided the offset image into many blocks. Each small block was cropped for edges and then calculated the L2 norm to obtain the offset of each small block. There were mainly two problems: one was that the rough offset was still too rough, and the local images needed to search for offsets that were not as small as imagined. The other was that the image contained a large number of parts without many edges, such as the sky, grass, and water surface. The offsets of these parts were easily abnormal and completely unreliable. These are not code problems but inherent in image processing. In this case, finding the most likely transformation is probably not as good as the already quite good edge alignment.
I think this idea is still good, so I tried some remedial measures. I did statistics on the gradients within the small blocks, and if they were below the threshold, the offset of the small block was considered unreliable. After running, I found some correlation, but the effect was still not good.
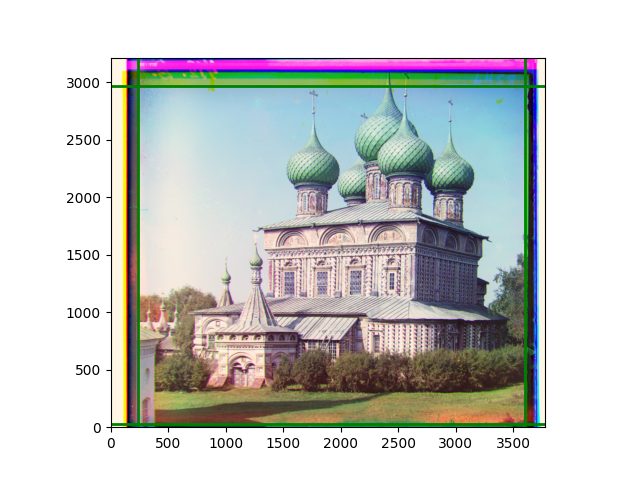
My view is that based on detailed features, if more external library functions are allowed, it is still possible to achieve the expected effect. For example, using library functions to directly obtain a list of feature points and matches. However, based on the existing code, I hope to complete the calculation of the affine transformation matrix in form. Since many places do not have effective edges, I obtained weights based on the L2 norm of the image itself, used the centers of those blocks as corresponding points, and used the library’s built-in functions to fit the affine transformation matrix and transform the image.
However, there was again the problem of dimension order, which took a lot of time to debug. The final discovery was that relying solely on these points often led to excessive rotation. I believe these problems are caused by the differences between the local and overall properties of the image. The image consists of exciting local parts and mundane backgrounds, but randomly selecting a sliding window from the image is likely to contain very monotonous content, making it difficult to match between different channels. Therefore, an interesting phenomenon is that in an image that can be well-aligned, randomly selected sliding windows are not always well-aligned.
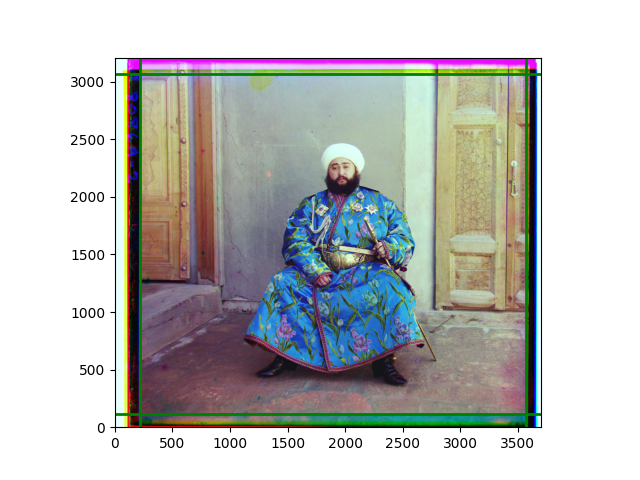
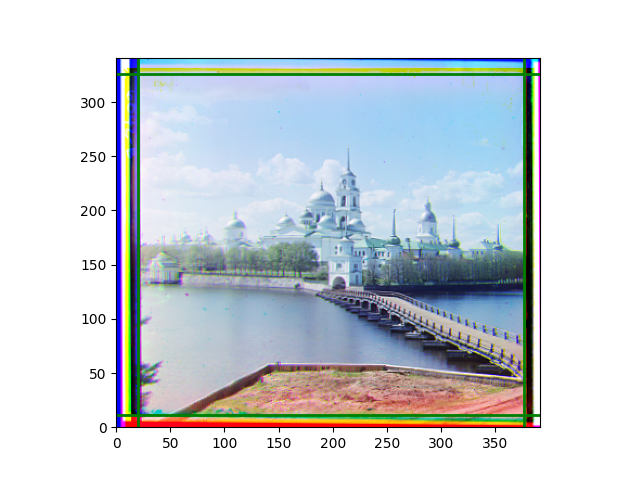
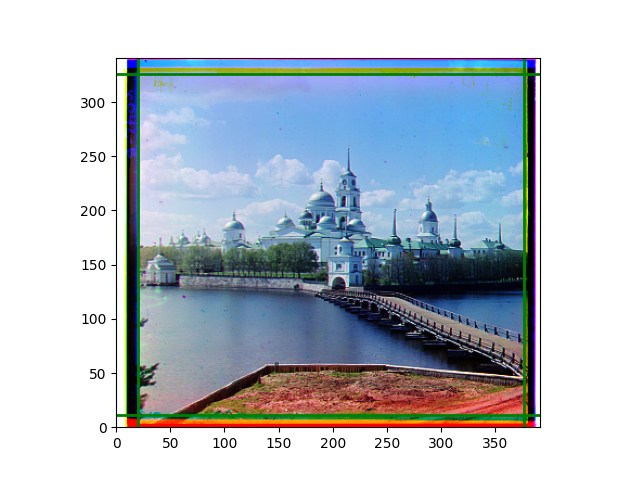
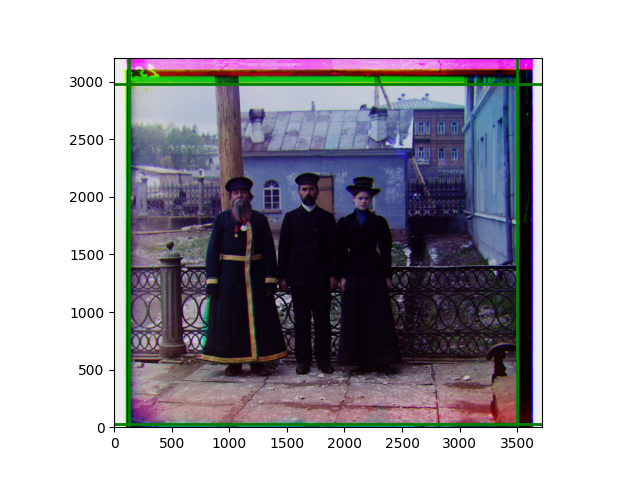
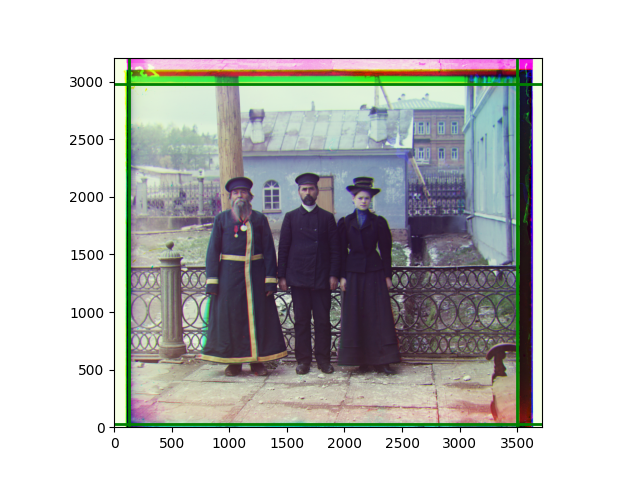
I later abandoned the idea of determining the transformation from scratch and used this code to add a small degree of flexibility to the previous pyramid results. The effect brought by the transformation was not very obvious, and slight rotation or distortion could only be seen after careful comparison. In fact, the original performance was already at a level where the human eye could hardly notice any problems. As mentioned earlier, although each local part was well-aligned, slight inconsistencies in the displacements of several local images could easily lead to excessive reactions in the transformation matrix. The most noticeable difference was in the color of the edges, but that was caused by the roll function.
Finally, I also performed gamma correction and white balance. Whether these improved the images is hard to say; in some cases, they were effective, but more often, they seemed to act merely as stylistic filters. Personally, I prefer the effect after gamma correction, but it’s difficult to have a universal standard for improvement.
The program can run directly, but it requires the appropriate folders to be placed on the computer desktop. Running on all given images takes about two to three minutes. Since I started late, the text part was written while thinking and doing, without a good summary. I apologize for that ☹. The images are displayed at the bottom of the webpage.
The images from left to right and top to bottom are: sobel, r, g, b, sobel, affine, gamma, gray.